ｼﾞｮｲｼﾞｮｲｼﾞｮｲ

ｼﾞｮｲｼﾞｮｲｼﾞｮｲｼﾞｮｲｼﾞｮｲ

Adam

Adam [1] を chainer で実装しました。

Adam の説明

少ない時間・空間計算量で高い性能を出すということで、深層学習の分野で最近よく使われている最適化手法です。

$\theta$ をパラメータに取る関数 $f(x,\theta)$ の（期待値）最小化を考えます。 $f$ の $\theta$ に対する勾配を $g$ とします。

一番元となったアルゴリズムは SGD ( stochastic gradient descent ) です。

SGD は以下のようにパラメータを更新するものでした。

$t \leftarrow 1$ とする
$x$ をサンプルする
$\theta_{(t)} \leftarrow \theta_{(t-1)} - \alpha \cdot g(x,\theta_{(t-1)})$
収束したら終了
$t \leftarrow t + 1$
2 に戻る

Adam では、 3 のステップを以下の処理に置き換えます。

$\displaystyle m_{(t)} \leftarrow \beta_{1} \cdot m_{(t-1)} + ( 1 - \beta_{1} ) \cdot g(x,\theta^{(t-1)})$
$\displaystyle v_{(t)} \leftarrow \beta_{2} \cdot v_{(t-1)} + ( 1 - \beta_{2} ) \cdot g(x,\theta^{(t-1)}) \odot g(x,\theta^{(t-1)})$
$\displaystyle \hat{m}_{(t)} \leftarrow \frac{m_{(t)}}{ 1 - \beta_{1}^{t} }$
$\displaystyle \hat{v}_{(t)} \leftarrow \frac{v_{(t)}}{ 1 - \beta_{2}^{t} }$
$\displaystyle \theta_{(t)} \leftarrow \theta_{(t-1)} - \alpha \cdot \frac{\hat{m}_{(t)}}{ \sqrt{\hat{v}_{(t)}} + \varepsilon }$

ここで、 $m_{(0)}, v_{(0)}$ は $0$ に初期化されているものとし、 $\odot$ は要素ごとの掛け算を表します。

論文では、 $\alpha = 0.001, \beta_{1} = 0.9, \beta_{2} = 0.999, \varepsilon = 10^{-8}$ 程度を目安としています。

1, 2 については、 $g$ と $g^{2}$ (要素ごとの自乗) の指数移動平均を求めています。

過去の結果をできるだけ使いたいが、パラメータが変化したことで分布も変化するので、このような指数移動平均を使っているのだと思います。

また、こうすることで時間と共に $f$ が変化するような問題にもうまく適合するようになるようです。

3, 4 では、正規化のようなことをしています。

例えば、 $g$ が一定値 $g_0$ をとるものとすると、 $\hat{m} = g_0$ となります。

5 が、 SGD における 3 に直接対応するものです。

$\varepsilon$ は $\hat{v}$ が極端に小さかったときに数値的な安定を保つためのものなのであまり深く考えなくても良いと思います。

$g$ の代わりに、移動平均を正規化した $\hat{m}$ を使い、 $\sqrt{\hat{v}}$ で割って変化量を正規化しています。

$\sqrt{\hat{v}}$ で割っていることで、 $f$ を定数倍しても、 $\theta$ の変化量は変わりません。

また、変化量はおおよそ $\alpha$ で抑えられます。

このようなスケールに対する不変性があるので、様々な問題に対して少ないハイパーパラメータのチューニングでうまく適合できるようです。

実装

Python 3.5.1 + chainer 2.0.0 を使って実装しました。

gist.github.com

実験

MNIST の分類を 3 層の全結合ニューラルネットワーク行いました。

f:id:joisino:20170719160803p:plain

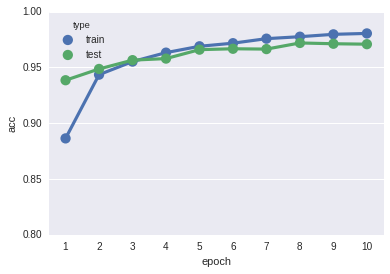
訓練データ、テストデータ共に、少ない反復回数で高い認識率を示しています。

最後に

何か間違いや質問などがあればお願いします。

最後まで読んでいただきありがとうございました。

参考文献

[1] Kingma, Diederik P. et al. (2015) Adam: A Method for Stochastic Optimization