ｼﾞｮｲｼﾞｮｲｼﾞｮｲ

ｼﾞｮｲｼﾞｮｲｼﾞｮｲｼﾞｮｲｼﾞｮｲ

Parikhの定理

この前 Parikh の定理（パリークの定理）を知ってびっくりしたので紹介します。

形式言語界隈では常識らしいです。

三行で説明して

文脈自由言語と正規言語は、単語を記号の度数で同一視（つまり記号の順番を無視する）と、同じクラスになるというものです。

具体的には準線形というクラスになります。

びっくりしませんか？僕はびっくりしました。

基本的な用語の定義

以下、終端記号の集合を \Sigma = \{ a_{1}, a_{2}, \dots, a_{k} \} とします。

線形部分集合

\mathbb{N}^{k} の元 x_{0}, x_{1}, \dots, x_{n} \in \mathbb{N}^{k} を用いて \{ x_{0} + \lambda_{1} x_{1} + \dots + \lambda_{n} x_{n} \mid \lambda_{1}, \dots, \lambda_{n} \in \mathbb{N} \} と表せる集合のことを線形部分集合(linear subset)といいます。

線形といいつつ x_{0} だけバイアスがあり \lambda_{i} \ge 0 なので錐みたいな感じです。

準線形部分集合

線形部分集合の有限族 L_{1}, L_{2}, \dots, L_{n} の和集合 L = L_{1} \cup L_{2} \cup \dots \cup L_{n} で表される集合のことを準線形部分集合 (semilinear subset)といいます。

語についての Parikh mapping

語 w \in \Sigma^{*} について、 w に a_{i} が登場する回数を m_{i} とします。このとき、 \Psi(w) = (m_{1}, m_{2}, \dots, m_{k}) となる \Psi : \Sigma^{*} \to \mathbb{N}^{k} を（語についての） Parikh mapping と呼びます。

言語についての Parikh mapping

言語 L \subset \Sigma^{*} について、 \Psi(L) = \{ \Psi(w) \mid w \in L \} となる \Psi : 2^{\Sigma^{*}} \to 2^{\mathbb{N}^{k}} を（言語についての） Parikh mapping と呼びます。記号の濫用ですが、混乱は生じないと思うので、語についての Parikh mapping と同じ記号 \Psi を用います。

Parikh の定理

準備が整ったので、ちゃんとした定義を述べます。

Parikh の定理

文脈自由言語 L について、 Parikh mapping \Psi(L) は準線形である

正規言語の Parikh mapping について

Parikh の定理の証明に入る前に、系として文脈自由言語と正規言語の Parikh mapping のクラスが一致することを示しておきます。

補題 1: 任意の線形部分集合 M について \Psi(L) = M となる正規言語 L が存在する。

\mathbb{N}^{k} の元 x_{0}, x_{1}, \dots, x_{n} \in \mathbb{N}^{k} について M = \{ x_{0} + \lambda_{1} x_{1} + \dots + \lambda_{n} x_{n} \mid \lambda_{1}, \dots, \lambda_{n} \in \mathbb{N} \} とします。

また、 \phi( (m_{1}, m_{2}, \dots, m_{n}) ) = a_{1}^{m_{1}} a_{2}^{m_{2}} \dots a_{k}^{m_{k}} と \phi : \mathbb{N}^{k} \to \Sigma^{*} を定義します。

例えば \phi( (3, 3, 4) ) = a_{1} a_{1} a_{1} a_{2} a_{2} a_{2} a_{3} a_{3} a_{3} a_{3} です。

X_{0} = \{ \phi(x_{0}) \}, X_{1} = \{ \phi(x_{1}) \}, \dots, X_{n} = \{ \phi(x_{n}) \} は有限集合なので正規です。正規言語のクラスはクリーネ閉包と連結について閉じているので X_{0} X_{1}^{*} \dots X_{n}^{*} は正規です。また、 \Psi(X_{0} X_{1}^{*} \dots X_{n}^{*}) = M となります。よって示されました。

系 2: 任意の準線形部分集合 M について \Psi(L) = M となる正規言語 L が存在する。

正規言語は和集合について閉じています。よって補題 1 より直ちに従います。

系 3: 任意の文脈自由言語 L について、 \Psi(L) = \Psi(L') となるような正規言語 L' が存在する

Parikh の定理より \Psi(L) は準線形です。よって系 2 より、 \Psi(L) = \Psi(L') となるような正規言語 L' が存在します。

Parikh の定理の証明

では証明に入りましょう。

文脈自由文法を非終端記号 N = \{ A_{1}, A_{2}, \dots, A_{n} \}、終端記号 \Sigma、生成規則 R、開始記号 A_{n} の組 G = ( N, \Sigma, R, A_{n} ) で定義します。

定義 4: \tilde{L}(G)

文脈自由文法 G において、全ての非終端記号を少なくとも一度ずつ用いて導出できる語の集合を \tilde{L}(G) とします。

後ろ向き推論によって問題を少し簡単にします。

補題 5: \Psi(\tilde{L}(G)) が準線形であることを示せば十分である。

N - \{ A_{n} \} の 2^{n-1} 通りの部分集合 N' について、新しい文法 G’ = ( N', \Sigma, R', A_{n} ) を作ります。ここで、導出規則 R' は、 R から非終端記号として N' の元のみが登場する規則を抜き出したものです。

これら全てについて \Psi(\tilde{L}(G')) が準線形であれば、それらの和集合 L(G) も準線形になります。

よって示されました。

以下扱う文脈自由文法 G = ( N, \Sigma, R, A_{n} ) を任意に一つとり固定します。

定義 6: T

T を、以下の 2 つの条件を満たす終端導出木（葉が全て終端記号である導出木）全体の集合とします。

  1. 全ての非終端記号が登場する
  2. 根からの任意のパスについて、各非終端記号は高々 |N| = n 回ずつしか登場しない

条件 1 から、 T の元によって導出される語は \tilde{L}(G) の元です。

また、条件 2 から木の深さは高々 n^{2} なので、 T は有限集合です。

定義 7: w_{i}

T により導出される語全体を w_{1}, w_{2}, \dots, w_{p} とします。 T は有限なのでこのような語も有限個です。

定義 8: \tilde{T}

\tilde{T} を全ての非終端記号が登場する終端導出木全体の集合とします。

この条件は定義 6 の条件 1 と同一なので、 T は \tilde{T} の部分集合です。

また、定義より語が \tilde{T} によって導出されることと \tilde{L}(G) の元であることは同値です。

定義 9: I

I を以下の 3 つの条件を満たす（特殊な）導出木全体の集合とします。

  1. 根は、非終端記号のいずれかである（開始記号 A_{n} である必要はない）
  2. 葉はちょうど 1 つを除き全て終端記号である。ちょうど 1 つある非終端記号は根と同じ記号である。
  3. 根からの任意のパスについて、各非終端記号は高々 |N| = n 回ずつしか登場しない（定義 6 の条件 2 と同一）

条件 3 より、 T の場合と同じく I は有限集合です。

定義 10: v_{i}

I による導出 A \to^{*} sAt ( s, t \in \Sigma^{*}, A \in N ) について、 v = st \in \Sigma^{*} 全体を v_{1}, v_{2}, \dots, v_{q} とします。 I は有限なのでこのような語も有限個です。

定義 11: L_{i}

L_{i} = \{ \Psi(w_{i}) + \lambda_{1} \Psi(v_{1}) + \dots + \lambda_{q} \Psi(v_{q}) \mid \lambda_{1}, \dots, \lambda_{q} \in \mathbb{N} \}

とします。定義より L_{i} は線形集合です。

Parikh の定理の証明

\Psi(\tilde{L}(G)) = L_{1} \cup L_{2} \cup \dots \cup L_{p} であることを示します。 L_{1} \cup L_{2} \cup \dots \cup L_{p} は準線形集合なので、これを示せば十分です。

両辺がもう一方に含まれることをそれぞれの方向について示します。

補題 12: L_{i} \subset \Psi(\tilde{L}(G))

\Psi(w_{i}) + \lambda_{1} \Psi(v_{1}) + \dots + \lambda_{q} \Psi(v_{q}) \in \Psi(\tilde{L}(G)) となることを \lambda_{1} + \dots + \lambda_{q} についての帰納法で示します。

w_{i} は T \subset \tilde{T} の元により導出されるので \tilde{L}(G) の元です。よって \Psi(w_{i}) \in \Psi(\tilde{L}(G)) となります。

\Psi(w_{i}) + \lambda_{1} \Psi(v_{1}) + \dots + \lambda_{q} \Psi(v_{q}) \in \Psi(\tilde{L}(G)) とするとき、 \Psi(w_{i}) + \lambda_{1} \Psi(v_{1}) + \dots + \lambda_{q} \Psi(v_{q}) + \Psi(v_{i}) \in \Psi(\tilde{L}(G)) を示します。

まず、帰納法の仮定より、 \Psi(w) = \Psi(w_{i}) + \lambda_{1} \Psi(v_{1}) + \dots + \lambda_{q} \Psi(v_{q}) であって、全ての非終端記号を使った終端導出木 S によって導出できる w \in \Sigma^{*} が存在します。

また、 v_{i} は I の元によって A \to^{*} s A t となるような部分的な導出によって v_{i} = st と表されます。

ここで、 S による導出によって登場する非終端記号 A を一度 A \to^{*} s A t と変形して、後は S と同様に導出を続けます。

これによって、導出される語 w' は、 \Psi(w') = \Psi(w) + \Psi(s) + \Psi(t) = \Psi(w) + \Psi(v_{i}) を満たします。

また、この時の導出木は S に登場する非終端記号を全て含むので、同様に全ての非終端記号を含み、 w' \in \tilde{L}(G) となります。

よって示されました。

補題 13: \Psi(\tilde{L}(G)) \subset L_{1} \cup L_{2} \cup \dots \cup L_{p}

\tilde{T} の元 S によって導出される語 w が \Psi(w) \in L_{1} \cup L_{2} \cup \dots \cup L_{p} となることを、木の大きさについての帰納法で示します。

まず、 S の根からのパスのうち同じ非終端記号が登場する回数が最も多いものの登場回数が |N| = n 回以下のとき、定義より S は T の元でもあるので、 w は w_{1}, w_{2}, \dots, w_{p} のいずれかに一致します。よって \Psi(w) \in L_{1} \cup L_{2} \cup \dots \cup L_{p} となります。

次に登場回数が n 回より大きいとき、 S の頂点であって、その頂点から葉方向に伸びる、同じ非終端記号を n + 1 個含むパスを持つような頂点のうち、根から最も遠い頂点（複数あればどれでもよい） v_{1} を選びます（少なくとも根は条件を満たすので、このような頂点は存在します）。

この n + 1 個ある非終端記号（ A とします）に対応する頂点を根から近い順に v_{1}, v_{2}, \dots, v_{n+1} とします。（ v_{1} 自身が A であることは少し考えれば分かります。）

S の部分木で、 v_{i} から v_{i+1} と終端記号を導出するものを S_{i}, S から S_{i} を取り除いたものを \tilde{S}_{i} とします（ややこしいので以下に図を掲載します）。

f:id:joisino:20171124102446p:plain

f:id:joisino:20171124102455p:plain

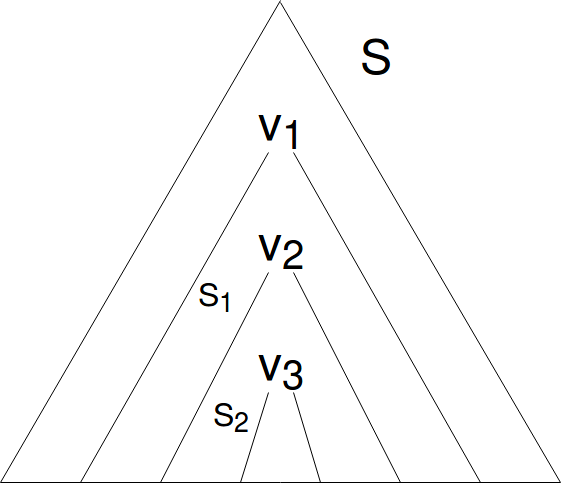
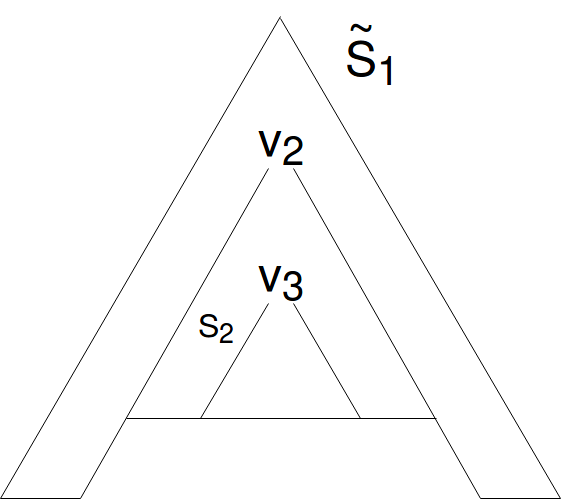
▲わかりやすい図

ここで、 v_{1} の子孫は、同じ非終端記号を n + 1 個含む、その頂点から葉方向に伸びるパスを持たないので、 S_{i} は I の元です。

また、 \tilde{S}_{i} のうち、 \tilde{T} に含まれるようなものが少なくともひとつ以上あることが以下のように分かります。

\tilde{S}_{i} が \tilde{T} に含まれないということは、定義より \tilde{S}_{i} に含まれない非終端記号があるということです。 A は必ず \tilde{S}_{i} に含まれていて、 S には全ての種類の非終端記号が出現することから、これは A 以外のいずれかの非終端記号の出現が全て S_{i} にあるということです。一方、 S_{i} は 1 \le i \le n の n 個の候補があります。これら全ての候補が（ n-1 個ある） A 以外のいずれかの非終端記号を全て含むということはありえません。よって、 \tilde{S}_{i} のうち、 \tilde{T} に含まれるようなものが少なくともひとつ以上あります。

\tilde{T} に含まれる \tilde{S}_{i} を 1 つとり、これが導出する語を w' とします。また、 S_{i} の導出が A \to^{*} sAt ( s, t \in \Sigma^{*}, A \in N ) のとき、 v_{j} = st とします。

帰納法の仮定より、 \Psi(w') \in L_{1} \cup L_{2} \cup \dots \cup L_{p} です。

また、 \Psi(w) = \Psi(w') + \Psi(v_{j}) なので \Psi(w) \in L_{1} \cup L_{2} \cup \dots \cup L_{p} です。

以上より示されました。

補題 12, 13 により、 \Psi(\tilde{L}(G)) = L_{1} \cup L_{2} \cup \dots \cup L_{p} となります。以上で証明は完了です。

最後に

いかがでしょうか。僕はかなりびっくりしました。

何か間違いや質問などがあればお願いします。

最後まで読んでいただきありがとうございました。

参考文献

[1] Parikh's theorem - Wikipedia

[2] http://www8.cs.umu.se/kurser/TDBC92/VT06/final/3.pdf