合同な凸図形でn要素ベン図を構成する方法 - ｼﾞｮｲｼﾞｮｲｼﾞｮｲ

この記事は Concrete Mathematics の演習問題 1.22 を元に作成しています。

ベン図とは複数の集合の関係を図式化したものです。例えば以下は 3 要素のベン図です。

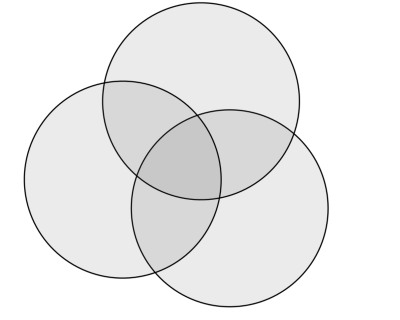
f:id:joisino:20210214180502p:plain

n 要素のベン図には n 個の図形があり、2ⁿ 個の領域に分かれ、それぞれの領域は含まれる図形の集合が異なるようになっています。

3 要素のベン図は上記のように円で描けるのですが、4 要素のベン図は円で描けないことが知られています。（4 つの円で 2⁴ = 16 個の領域を構成するのが無理なため。）

どんな図形を使ってもよければ多要素のベン図を構成するのは容易ですが、任意の n について合同な凸図形のみで n 要素のベン図構成することは可能でしょうか？

取っ掛かりのなく難しそうな問題ですが、実はキレイに解けることが知られています。

準備: de Bruijn 列

構成にあたって de Bruijn 列というものを使います。

定義: de Bruijn 列

長さ $2^n$ の 01 文字列 $S \in \{0, 1\}^{2^n}$ が要素数 $n$ の de Bruijn 列であるとは、S を二回連結させた文字列 SS の $i = 1, \cdots, 2^n$ 番目から始まる長さ $n$ の部分文字列が長さ $n$ の 01 文字列を全て網羅していることをいう。つまり、 $\{SS[i: i+n ] | i = 1, \cdots, 2^n\} = \{0, 1\}^n$ 。

定義のため S を二つ並べましたが、S の最初と最後をくっつけて円環にしたときに全ての長さ n の部分文字列が異なる、という見方もできます。（この見方を後で使います。）

例: 3 要素の de Bruijn 列

S = 00010111 は 3 要素の de Bruijn 列です。なぜなら、SS = 0001011100010111 であり、最初の 8 つの長さ 3 の部分文字列 000, 001, 010, 101, 011, 111, 110, 100 に長さ 3 の 01 列が全て登場するからです。ここで例えば 4 つ目の 101 は 000[101]1100010111 のカッコの中、8 つ目の 100 は 0001011[100]010111 のカッコの中に対応しています。

補題: 任意の正整数 n に対し n 要素の de Bruijn 列が存在する

（グラフ理論の知識が必要なので分からなければ読み飛ばしてください。）de Bruijn グラフというラベル付き有向グラフを使い $n \ge 2$ の場合を示します。n 次の de Bruijn グラフは 2ⁿ 個ノードを持ち、各ノードはユニークな 01 文字列がラベルされています。各ノードの 0 枝はラベルの先頭文字を取り除いて末尾に 0 を追加したラベルのノードに繋がっています。例えば 001 は 010 に繋がります。1 枝も同様に先頭文字を取り除いて末尾に 1 を追加したラベルのノードに繋がっています。以下が 3 次の de Bruijn グラフです。

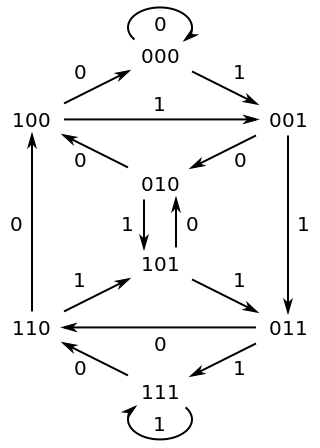
f:id:joisino:20210214175956p:plain

これは直感的にはオートマトンのようなものを表していると思ってください。このグラフの各辺は元ノード + 辺ラベルからなる長さ n + 1 の文字列を表しています。例えば、S = 000 からはじまり、1 枝を辿ると文字列 0001 が完成し、今の状態が 001 になります。ここから 0 枝を辿ると文字列 0010 が完成し、状態 010 に移ります。なので、n 次の de Bruijn グラフのオイラー路が n + 1 要素の de Bruijn 列に対応します。de Bruijn グラフは入次数と出次数が全て 2 で強連結なのでオイラー路を持ちます。よって、n 要素の de Bruijn 列が存在します。

（ちなみに n 次の de Bruijn グラフのハミルトン路は n 要素の de Bruijn 列に対応しますが、オイラー路の方が簡単なので普通はオイラー路を考えます。）

定理: 合同な凸図形で n 要素のベン図を構成できる

それでは実際に構成します。まず正 2ⁿ 角形 P と n 要素の de Bruijn 列 S を用意し、P の各辺を順番に S で 0 か 1 にラベル付けていきます。次に、1 にラベル付けた辺を凸性を保たせながら少しだけ外側に膨らませます。こうしてできた図形を n 個コピーしてそれぞれ辺 1 個、2 個、...、n 個分回転させると n 要素のベン図が出来上がります。なぜなら、一つの辺に注目すると 1 ラベルが付いている図形だけが外側に膨らんでおりそれらの図形のみから囲われる領域があります。この辺に付いているラベルを 1 つ目の図形から順に並べると de Bruijn 列の部分文字列に対応し、これは de Bruijn 列の性質から全てパターンが 1 回ずつ登場します。

例えば n = 3 の場合以下の図のようになります。

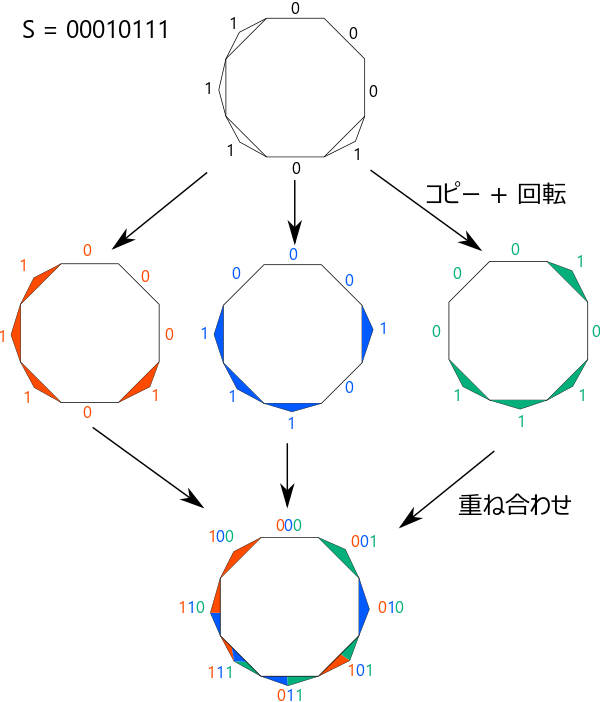
f:id:joisino:20210214193109p:plain

おわりに

de Bruijn 列の性質も面白いし、ガジェットの作り方もシンプルで面白いので紹介しました。楽しんでいただければ幸いです。