明日、KMC の組合せ最適化読書会でやる予定なのですが、少し調べた限りでは日本語の解説が見つからなかったので書いてみます。(注:組合せ最適化本体には O(nm) のアルゴリズムしか載っていません。)
こういうアルゴリズムに慣れていない人向けに書いたつもりなのでプロ各位にはまどろっこくて分かりづらい表現になったかもしれません。ゆるして。
最小全域有向木について
辺にコストのついた有向グラフが与えられて一つの頂点が指定されたとき、その頂点を根とする全域有向木でコスト最小のものを求める問題です。
根用の頂点を追加して、各点にコスト INF の辺を張れば頂点を指定しない最小全域有向木が解けます。コスト 0 で張ると最小有向森です。
有名な解法に Edmonds / Chu-Liu のアルゴリズムがあります。この計算量は O( nm ) で、組合せ最適化や Spaghetti Source - 最小全域有向木(Chu-Liu/Edmonds) に載っています。今から説明する O( m log n ) の解法は Tarjan [1977] によるもので、このアルゴリズムの亜種(というか高速化しただけ)です。
アルゴリズム
- 根以外の頂点を適当に選びます
- 今いる頂点 v に入ってくる(自己ループでない)辺のうちコストが一番小さい辺 ( u -> v ) を取ります。今いる頂点が圧縮された頂点なら、もとのサイクルで v に入ってくる辺を使う辺から除きます。u に移り、( u -> v ) を使う辺に追加します。
- 使う辺でサイクルができたら、サイクルを一点に圧縮します。このとき、サイクル外からサイクル上の頂点 w に入ってくる辺のコストを、w に入ってくるサイクル辺のコストだけ減らします。
- まだ根と繋がらなかったら 2 に戻ります。繋がったときは、他に頂点が無いなら終了。まだあるなら適当に頂点を選んで 2 に戻ります。
やることはすごく簡単です。少し下で解説をしているのでこれを読んで分からなければそっちを読んでみてください。(むしろこれだけで分かったらすごい)
解説
有向木では、根以外の入次数は 1 です。(もちろん根は 0 です。)なので、各頂点について入ってくる辺をちょうど一つ選ぶわけです。このアルゴリズムでは、手順 2 で貪欲に一番コストが小さい辺を選んでいっています。サイクルができなければこれが一番良いことはすぐに分かると思います。
厄介なのはサイクルができたときです。サイクルができた時は、そこで詰んでしまうので、サイクルを「開いて」やらなければいけません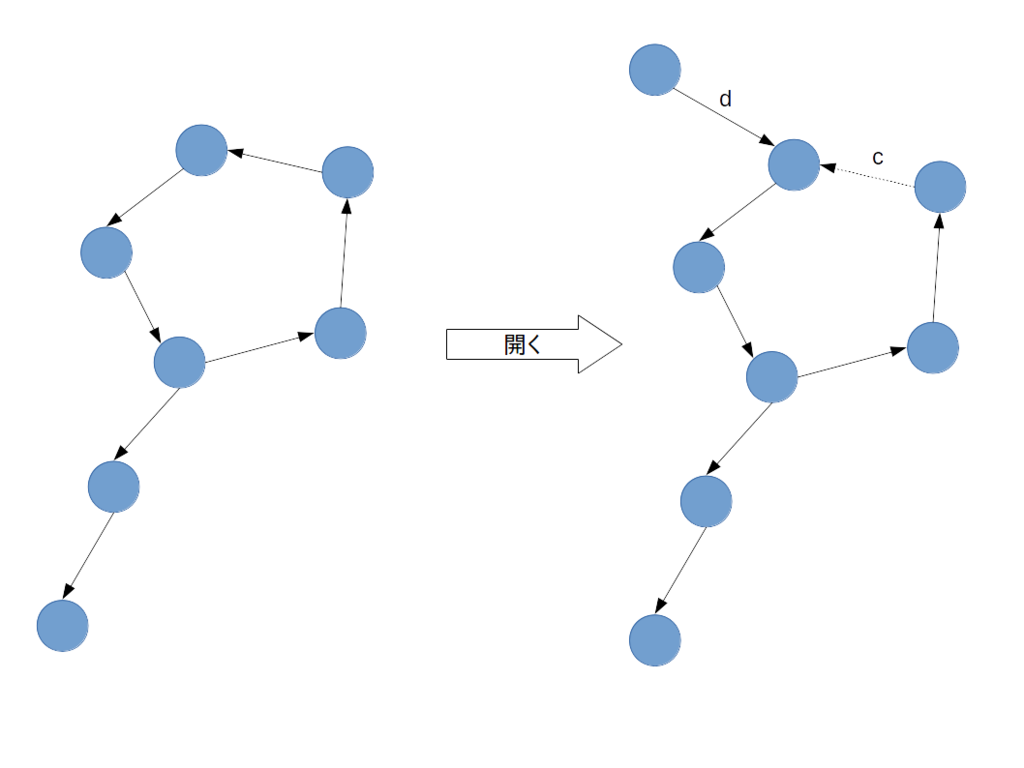
サイクルに繋がる辺を選ぶ訳ですが、上の図のように開くと総コストが d - c だけ増えます。(コスト c の辺を使うのをやめてコスト d の辺を使うため。)このアルゴリズムではこのコストについて貪欲に小さいものを選びます。アルゴリズムの手順 3 で「このとき、サイクル外からサイクル上の頂点 w に入ってくる辺のコストを、w に入ってくるサイクル辺のコストだけ減らします。」と言っているのはそういうことです。(「サイクル外からサイクル上の頂点 w に入ってくる辺のコスト」は図の d に対応し、「w に入ってくるサイクル辺のコスト」は図の c に対応します。)
サイクルができるたびに上のように対応して、サイクル(だったもの)はそれ以降変更しないように一点に圧縮してしまいます。(これは、正当性の証明のところで示すようにサイクルの一辺以外を全て含むような最小全域有向木があるので OK です。)
入ってくる辺を貪欲に選んで、サイクルを貪欲に切って圧縮するというのは Edmonds のアルゴリズムも同じです。違うところは、Edmonds では全部の頂点について入ってくる辺を選んでから圧縮するのを繰り返しているのに対し、このアルゴリズムでは DFS の要領で一つずつ頂点を処理していくことです。
現在の頂点から辺を逆に辿ってパスが伸びるか、サイクルができても圧縮してしまうので、現在の処理している辺たちは常にパスのように見えることになります。
こうすると、辺を辿るたびに、パスが 1 つ伸びるか、サイクルができて、サイクルの大きさくらいの頂点が消えるので、 2n ステップくらいで止まることが分かります。
正当性の証明
Edmonds のアルゴリズムの正当性の証明とほとんど同じです。そっちを知っている人はこれも証明できると思うので自力でやってみてもいいかもしれません。
証明は圧縮する回数についての帰納法で行います。
圧縮する回数が 0 回(圧縮しない)とき
これは、解説のところでも言及しましたが、ほとんど明らかだと思います。
このアルゴリズムで得られた有向木 T と、任意の有向木 S を比べたとき、各頂点に入ってくる辺同士についてコストを比べると、T の辺は入ってくる辺の中で一番コストが小さいものを選んでいるので、もちろん T の辺のコストが S の辺のコスト以下になります。ということは、総和をとっても T 全体のコストは S 全体のコスト以下です。
圧縮する回数が k + 1 回のとき
まず、最初に圧縮することになるサイクルを C とします。 C は L 本の辺からなるとします。
ここで、なんとサイクル C の辺のうち、L - 1 本の辺を使う最小全域有向木が存在することがいえます。(この証明は組合せ最適化にも載っています。慣れない人には少し難しいかもしれないので分からなかったら認めてしまって次に進んでも良いかもしれません。飛ばす場合は「補題の証明終わり」というところまで進んでください。)
最小全域有向木のうち、サイクル C の辺を使う本数が最も多いものを A とします。C の辺のうち K ( >= 2 ) 本使わないがあると仮定します。
C の辺のうち、A で使われていない辺を、一周回る順番に ( a_1, b_1 ), ..., ( a_K, b_K ) とします。ここで、i = 1, 2, ..., K について A には b_i から b_{i-1} にパスがあることを示します。( i = 1 のときには i-1 は K を表していると思ってください。)
( a_i, b_i ) が使われていないのだから、A には b_i に入ってくる他の辺 e があるはずです。
e を使うのやめて ( a_i, b_i ) を使うことにしてみます。
( a_i, b_i ) のコストは b_i に入ってくる辺の中で一番小さいのでコストの総和は変更前以下になります。変更後もちゃんと有向木だったとすると、コストが真に小さくなっても A が最小であることに反するし、同じでも C のうち使う辺の本数が 1 本多いので、 A のとり方に違反します。
考えられるのは使う辺を変えたことでサイクルができてしまったということです。
これは、A において、b_i から a_i にパスがあったということです。a_i からそのパスを逆向きにたどって行くと以下の図から分かるように b_{i-1} にたどり着きます。(入次数が 1 なので一意にたどれます。また、(a_{i-1}, b_{i-1}) は使わない C の辺のうち一つ前の辺なので、間の辺は全て A でも使われています。)
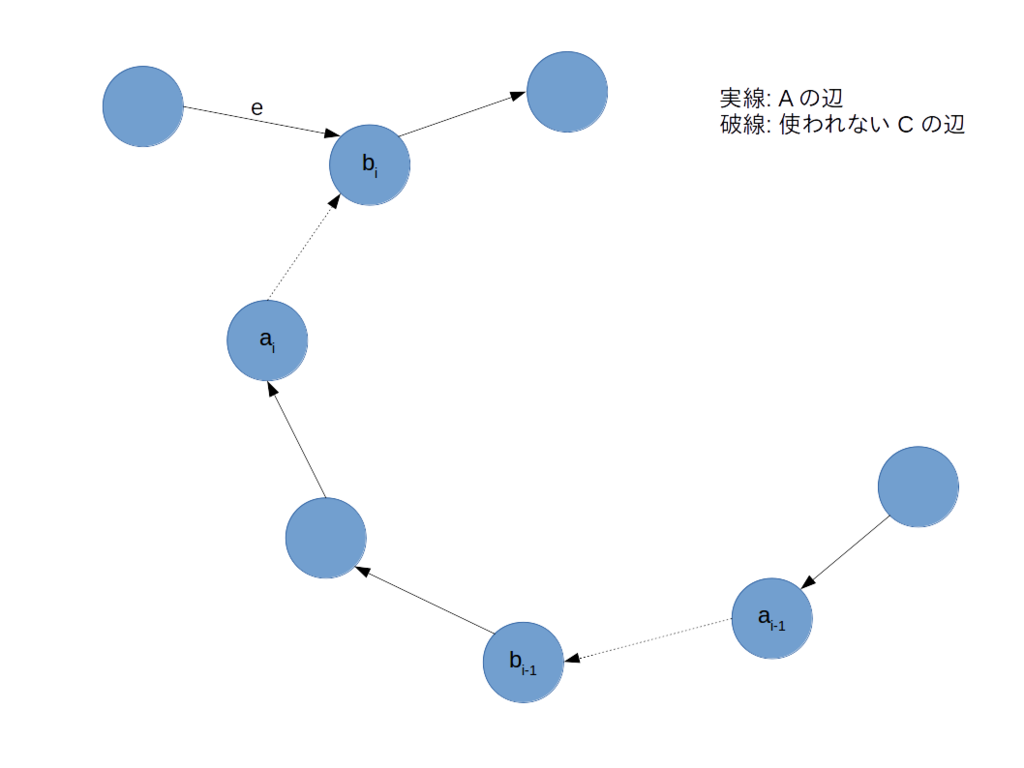
つまり、A 上には b_i から b_{i-1} にパスがあるということです。(b_i から a_{i-1} へのパスの一部分。)
これでパスの存在は示せました。
しかし、これは b_K からb_{K-1} にパスがあり、b_{K-1} から b_{K-2} にパスがあり、...、b_1 から b_K にパスがあるということになり、A にサイクルがあるということになります。
これは A が有向木であるという仮定に反します。
よって、最小全域有向木のうち、サイクル C の辺を使う本数が最も多いものは L - 1 本の辺を使うということになります。
補題の証明終わり
もとの証明に戻ります。圧縮する回数が k+1 回のときにアルゴリズムで得られた有向木が最小全域有向木であることを示すのが目的でした。
このアルゴリズムで得られた有向木を T とし、サイクル C を圧縮したときにできるグラフ(以下圧縮グラフと呼びます)で T に相当する有向木を T' とします。帰納法の仮定より、 T' は圧縮グラフでの最小全域有向木です。
補題により存在が示された、C の辺のうち L - 1 本を使う最小有向木を T* とし、圧縮グラフで T* に相当する有向木を T*' とします。
ここで、 T のコストは T' のコストにサイクル C に含まれる全ての辺のコストの和を足したものとなります。T* についても同様に T*' のコストに C のコストを足したものになります。
これは、 T' で C に相当する部分以外のコストは同じで、 C は、1 本以外全て使うことになりますが、使わない辺については C に入ってくる辺のコストの変更によって調整されているので、このようになります。
よって、( T のコスト ) = ( T' のコスト ) + ( C のコスト ) <= ( T*' のコスト ) + ( C のコスト ) = ( T* のコスト )
となり、 T が最小全域有向木であることが分かります。真ん中の不等号は T' が圧縮グラフ上での最小全域有向木であることからです。
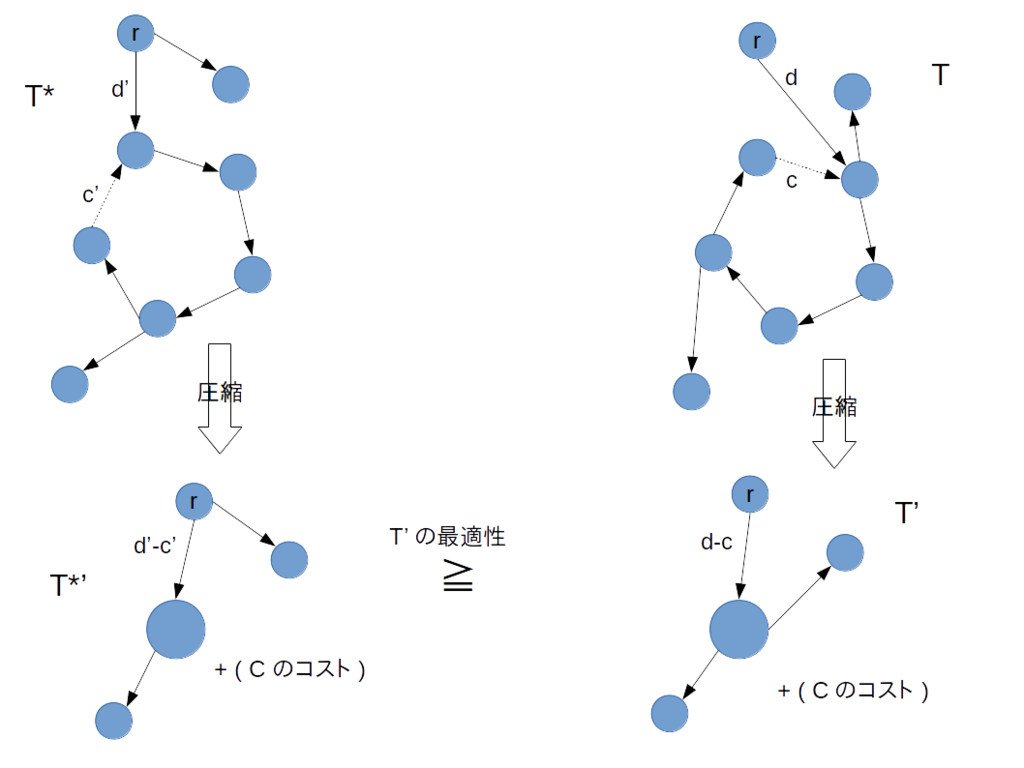
以上、帰納法によって正当性が示されました。
計算量
計算量を調べます。
解説のところで言及したように、1 ステップ ごとにパスが伸びるか、頂点がマージされて減るのでアルゴリズムの手順 2, 3 を実行する回数は O(n) 回です。
各頂点について入ってくる辺を隣接行列でもって愚直に管理するとします。手順 2 で最小値を求めるのは毎回 O(n) で、これは O(n) 回行われます。手順 3 で圧縮するのも、1 つの点につき O(n) でマージできて、合計高々 n 頂点しかマージされないので、結局全体の計算量は O(n^2) になります。
密グラフでこのアルゴリズムを走らせたいときはこれ以上速くなりようがないのでこれで終了です。
次に疎グラフで O( m log n ) を達成するやり方を考えます。
dijkstra 法などを学んだ人ならなんとなく分かると思いますが、辺をヒープ(prioirty queue)で管理します。
こうすると手順 2 で最小値を求めるのは毎回 O(1) になります。
問題は圧縮です。ヒープをうまくマージしたりコストを一様に減らしたりする方法なんてあるのかと思いますがあります。
一つには、マージテクを使うとできます。これで O( m log n + n log^2 n ) とかになります。
もう一つには、meldable heap というものを使います。これはマージが効率よくできるヒープのことで、leftist heap や skew heap などがあります。blog - Leftist Heap & Skew Heap に詳しいのでそちらを参照してみてください。これで O( log n ) でマージできます。また、コストを一様に減らす方法ですが、ヒープのノードに一様に足された数を持っておいてマージするときに遅延伝播すればうまくいきます。(segtree の遅延伝播と全く同じです。)これで全体で O( m log n ) になります。おめでとうございます。
具体的な実装例は使い道のところを参照してみてください。
ちなみに、fibonacci heap を使うとマージが O(1) でできます。コストを一様に減らす解析は読んでないので良く分かっていませんが Gabow et al. [1986] によると全体で O( m + n log n ) になるらしいです。誰か読んで分かりやすく教えて。
使い道
競技プログラミングでは今のところあまり実用性はないかもしれませんが、とりあえず首都(The Capital | Aizu Online Judge)をアルゴリズムパンチで殴り倒せます。
実装例です。多めにコメントを書きました。MSA という関数が、 r を根とする最小全域有向木のコストを求める関数です。「ここが本質です。」と書いてあるループ部分が最小全域有向木のメインの部分です。
終わりに
この記事を書くまでは最小全域有向木は無向の最小全域木よりも(少なくとも競技プログラミングで使うようなアルゴリズムでは)有意に計算量が大きいものだと思っていたんですが、割と簡単なアルゴリズムで似たような計算量が達成できるのにビックリしました。
最小全域有向木を使う問題はあんまり見ないですが、n = 10^5 とかで割と簡単に書けるので使いようがあるんじゃないかと思いました。(浸透しないとただの知識ゲーだけど)
ここが分からないとかここ間違ってるよとかあれば気軽に言ってください。
最後まで読んでいただきありがとうございました。
(1/11 23:33 マージテクでも少しいい感じにできるよということなど少し追記しました)
参考文献
[1] B.コルテ, J.フィーゲン [2012]: 組合せ最適化 第二版. 丸善, 2012, 第 6 章.
[2] Gabow, H.N., Galil, Z., Spencer, T., and Tarjan, R.E. [1986]: Efficient algorithm for finding minimum spanning trees in undirected and directed graphs. Combinatorica 6 (1986), 109-122
[3] Tarjan, R.E. [1977]: Fining optimum branchings, Networks (1977), 25-35