ケイリーの公式の証明6種類 - ｼﾞｮｲｼﾞｮｲｼﾞｮｲ

ケイリーの公式の証明たちの紹介です。

ケイリーの公式とは

ケイリーの公式とは $n$ 頂点のラベル付きの木の総数 $T(n)$ が $T(n) = n^{n-2}$ であるという公式のことです。

ここで、ラベル付きであるとは、それぞれの頂点を区別するということです。

たとえば $n = 3$ のとき、頂点を区別しない場合は長さ $3$ のパスのみの $1$ 通りですが、ラベル付きの木の場合は $1 - 2 - 3$ , $2 - 1 - 3$ , $1 - 3 - 2$ の $3 (= 3^{3-2} = T(3))$ 通りです。

証明 1 (プリューファーコード) [1]

おそらく一番有名な証明です。

$n$ 頂点のラベル付きの木の集合から $\{ 1, 2, \ldots, n \}^{n-2}$ への全単射を以下のように構成します。

最もラベルが小さい葉を木から取り除き、その葉と繋がっていた頂点のラベル $a_{1}$ を数列の最初の値とします。

続けて、最もラベルが小さい葉を木から取り除き、その葉と繋がっていた頂点のラベル $a_{2}$ を数列の $2$ 番目の値とします。

以下同様に頂点が $2$ つになるまで操作を続けます。

こうしてできた数列 $a_{1}, a_{2}, \ldots, a_{n-2}$ が木の値となります。

この数列をプリューファーコードといいます。

例えば、以下の木のプリューファーコードは $3, 2, 6, 6$ となります。

f:id:joisino:20170819151034p:plain

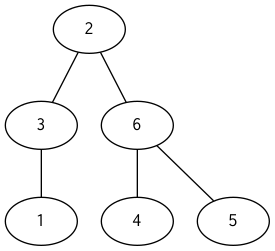
これの逆写像は以下のように与えられます。

まず、辺のない $n$ 頂点を用意します。

次に、 $a_{1}, a_{2}, \ldots, a_{n-2}$ に含まれない値のうち、最も小さいものを $b_{1}$ とし、 $a_{1}$ と $b_{1}$ を繋ぎます。

続けて、 $b_{1}, a_{2}, a_{3} \ldots, a_{n-2}$ に含まれない値のうち、最も小さいものを $b_{2}$ とし、 $a_{2}$ と $b_{2}$ を繋ぎます。

続けて、 $b_{1}, b_{2}, a_{3}, a_{4} \ldots, a_{n-2}$ に含まれない値のうち、最も小さいものを $b_{3}$ とし、 $a_{3}$ と $b_{3}$ を繋ぎます。

以下同様に木を構成していきます。

最後に、 $b_{1}, b_{2}, \ldots, b_{n-2}$ に含まれていない $2$ 頂点を繋いで完成です。

これが逆写像になっていることは以下のようにわかります。

まず、プリューファーコードに登場する頂点は元の木の内点で、かつ元の木の内点を全て尽くしています。

なぜなら

$a_{i}$ は $i$ 番目の操作の時点で葉とつながっている点なので、これが葉であると、操作後に頂点数が $1$ の成分になってしまうので矛盾です。よって全ての $a_{i}$ は内点です。
全ての内点は、操作のどこかの時点で葉になり、 $2$ 頂点以外は取り除かれていきます。少なくともその頂点が葉になった瞬間においてコード中に登場するはずなので、全ての内点を尽くしています。

以上より、逆に $a_{1}, a_{2}, \ldots, a_{n-2}$ に含まれない値は初期状態において葉であって、全ての葉を尽くしています。

そのうち最もラベルの小さい頂点は順写像において最初に取り除かれた頂点で、 $a_{1}$ と繋がっていたはずです。

以下帰納的に順写像の操作に対応する辺が見つかっていきます。

最後は、順写像の操作で取り除かれなかった頂点を結べば完成となります。

全単射が存在するということは要素の数が等しいということです。

$\{ 1, 2, \ldots, n \}^{n-2}$ の要素数はもちろん $n^{n-2}$ なので $T(n) = n^{n-2}$ となります。

証明 2 (もうひとつの全単射) [2]

もうひとつ全単射を使った証明を紹介します。

今度は $\{ 1, 2, \ldots, n \}^{n}$ から、 $n$ 頂点からなるラベル付きの木であって $1$ 頂点に赤い印がついていて $1$ 頂点が星形である木への全単射を構成します。

ここで、赤の頂点と星の頂点は同じ頂点でもかまいません。

ラベル付きの木を固定すると赤の頂点と星の頂点の選び方は $n^{2}$ 通りあるので、値域の要素数は $T(n) n^{2}$ で、定義域の要素数は $n^{n}$ なので、これらが等しければケイリーの公式の証明が完了します。

数列 $(a_{1}, a_{2}, \ldots, a_{n})$ を入力とします。

$1 \le i \le n$ について $i$ から $a_{i}$ へ辺があるような $n$ 頂点 $n$ 辺からなるグラフを考えます。

全ての出次数が $1$ であるグラフは functional graph と呼ばれ、サイクルに木がついた連結成分がいくつかあるような形になります。

例えば $7, 4, 8, 1, 7, 4, 4, 3$ のときグラフは以下のようになります。

f:id:joisino:20170819161216p:plain

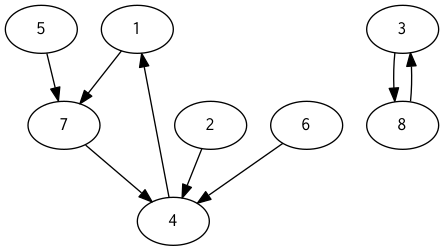
ここで、サイクル上の頂点をソートして並べたものを $b_{1}, b_{2}, \ldots, b_{k}$ とします。

上の例の場合 $1, 3, 4, 7, 8$ となります。

出力の木としては、 $a_{b_{1}}, a_{b_{2}}, \ldots, a_{b_{k}}$ をこの順に並べてパスとし、残りは functional graph と同様に繋げます。赤の頂点は $a_{b_{1}}$ を選び、星の頂点は $a_{b_{k}}$ を選びます。

上の例の場合は以下のようになります。

f:id:joisino:20170819162001p:plain

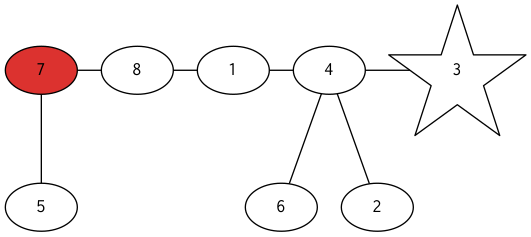
逆写像は以下のように構成します。

まず、木のうち、赤の頂点から星の頂点までの（一通りしかない）パスをとって、 $c_{1}, c_{2}, \ldots, c_{k}$ と順に並べます。

パス上の頂点のラベルをソートした数列を $b_{1}, b_{2}, \ldots, b_{k}$ とします。

$1 \le i \le k$ について、元の数列の $b_{i}$ 番目の値が $c_{i}$ であることが分かります。

パス以外の頂点は、パス上の頂点を根とした根付き木を考え、頂点 $v$ の親が $u$ のとき、元の数列の $v$ 番目の値が $u$ となることが分かります。

これで復元できました。

証明 3 (double counting) [2] [3]

この証明もかなり有名な証明です。

wikipedia にもこの証明が載っています。

頂点にも辺にもラベルが付いた $n$ 頂点からなる根付き木の総数 $U(n)$ を二通りの方法で数えます。

一つは、 $T(n)$ を使う方法です。ラベル付きの木を固定したとき、根の選び方が $n$ 通り、辺へのラベルの付け方が $(n-1)!$ 通りあるので、 $U(n) = T(n) \cdot n \cdot (n-1)!$ となります。

もうひとつは辺を $1$ つずつ追加していって逐次的に木を構成していく方法です。 $i$ 番目に追加した辺のラベルを $i$ とします。

辺のない $n$ 頂点からなるグラフを用意します。

最初の辺は、親の選び方が $n$ 通りあって、子の選び方は自分以外の $n-1$ 通りです。

$2$ つ目の辺は、親の選び方がこれも $n$ 通りあります。子の選び方は、根でない頂点を選ぶとその頂点の親が $2$ つになってしまうのでだめです。自分が属している木の根も、ループができてしまうのでだめです。よって、子の候補は $n-2$ 個となります。

同様に、 $1 \le i \le n-1$ について $i$ 番目の辺は、親の選び方が $n$ 通り、子の選び方が $n-i$ 通りとなります。

よって、 $U(n) = \Pi_{i=1}^{n-1} n (n-i) = n^{n-1} \cdot (n-1)!$ となります。

これが $T(n) \cdot n \cdot (n-1)!$ と等しいので $T(n) = n^{n-2}$ となります。

証明 4 (行列木定理) [2]

行列木定理を使った証明です。

ラベル付きの木の総数と $n$ 頂点完全グラフ $K_{n}$ の全域木の総数は同じです。

$K_{n}$ のラプラシアン行列は

$$ \displaystyle \left[ \begin{array}{rrr} n-1 & -1 & -1 & \ldots & -1 \\ -1 & n-1 & -1 & \ldots & -1 \\ -1 & -1 & n-1 & \ldots & -1 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -1 & -1 & -1 & \ldots & n-1 \end{array} \right] $$

となります。行列木定理より、 $T(n)$ はこの行列の任意の余因子と一致します。

$(1, 1)$ 余因子をとりましょう。

$(1, 1)$ 余因子はもとの行列から $1$ 行目と $1$ 列目を取り除いた $(n-1) \times (n-1)$ 行列の行列式です。

まず、 $2$ 行目から $n-1$ 行目を $1$ 行目に足します。すると $1$ 行目が全て $1$ になります。

$$ \displaystyle \left| \begin{array}{rrr} 1 & 1 & 1 & \ldots & 1 \\ -1 & n-1 & -1 & \ldots & -1 \\ -1 & -1 & n-1 & \ldots & -1 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -1 & -1 & -1 & \ldots & n-1 \end{array} \right| $$

次に、 $1$ 行目を $2$ 行目から $n-1$ 行目に足します。

$$ \displaystyle \left| \begin{array}{rrr} 1 & 1 & 1 & \ldots & 1 \\ 0 & n & 0 & \ldots & 0 \\ 0 & 0 & n & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & n \end{array} \right| $$

この式の値は $n^{n-2}$ なので、 $T(n) = n^{n-2}$ となります。

証明 5 (漸化式) [2]

より一般的な問題を漸化式と帰納法によって解きます。

ラベルの集合の、要素数 $k$ の部分集合 $A$ を任意にとります。

$A$ に含まれている頂点が互いに異なる連結成分に属するようなラベル付き森の数を $S(n,k)$ とします。

これは $A$ の要素数にしかよらないので well-defined です。

便宜上 $S(0,0) = 1, S(n,0) = 0 ( n > 0 )$ とします。

$S(n,k) = k \cdot n^{n-k-1}$ (*) であることを示します。

$T(n) = S(n,1)$ なので、これが示せればケイリーの公式は示されます。

ラベルの集合を $\{ 1, 2, \ldots, n \}$ とし、 $A = \{ 1, 2, \ldots, k \}$ としたときに $S(n, k)$ で数える森を $1$ つ固定します。

この森で頂点 $1$ と繋がっている頂点を $B = \{ a_{1}, a_{2}, \ldots, a_{l} \}$ とします。

このときこの森から頂点 $1$ を取り除いてできる森は、ラベルの集合を $\{ 2, 3, \ldots, n \}$ とし $A = \{ 2, 3, \ldots, k, a_{1}, a_{2}, \ldots, a_{l} \}$ としたときに $S(n-1,k+l-1)$ で数える要素になります。

逆にラベルの集合を $\{ 2, 3, \ldots, n \}$ とし $A = \{ 2, 3, \ldots, k, a_{1}, a_{2}, \ldots, a_{l} \}$ としたとき、新たに頂点 $1$ を加えて $a_{1}, a_{2}, \ldots, a_{l}$ とつなげると、先ほど考えていた $S(n, k)$ で数えた森に対応します。

つまり、 $S(n,k)$ で数える森は、 $A$ と交わらない頂点集合 $B$ ごとに $S(n-1,k+|B|-1)$ 個の森と対応づいているということです。

以上の考察から

$\displaystyle S(n,k) = \sum_{l=0}^{n-k} \binom{n-k}{l} S(n-1, k+l-1)$

となります。これは $B$ として、 $A$ 以外の要素 $n-k$ 個から $l$ 個選ぶというのを $l = 0, 1, \cdots n-k$ について足しあわせているということです。

この漸化式を使って帰納法により (*) を示しましょう。

$\begin{align*} S(n,k) &= \sum_{l=0}^{n-k} \binom{n-k}{l} S(n-1, k+l-1) & \\ &= \sum_{l=0}^{n-k} \binom{n-k}{l} (k+l-1) (n-1)^{n-k-l-1} & ({\rm 帰納法の仮定より})\\ &= \sum_{l=0}^{n-k} \binom{n-k}{l} (n-1-l) (n-1)^{l-1} & (l = n - k - l {\rm と変換}) \\ &= \sum_{l=0}^{n-k} \binom{n-k}{l} (n-1) \cdot (n-1)^{l-1} - \sum_{l=0}^{n-k} \binom{n-k}{l} l \cdot (n-1)^{l-1} & ({\rm 分配}) \\ &= \sum_{l=0}^{n-k} \binom{n-k}{l} (n-1)^{l} - \sum_{l=0}^{n-k} \binom{n-k}{l} l \cdot (n-1)^{l-1} & \\ &= (n-1+1)^{n-k} - \sum_{l=0}^{n-k} \binom{n-k}{l} l \cdot (n-1)^{l-1} & ({\rm 二項定理})\\ &= n^{n-k} - \sum_{l=0}^{n-k} \binom{n-k}{l} l \cdot (n-1)^{l-1} & \\ &= n^{n-k} - \sum_{l=1}^{n-k} \binom{n-k}{l} l \cdot (n-1)^{l-1} & (l=0 {\rm のとき} 0) \\ &= n^{n-k} - (n-k) \sum_{l=1}^{n-k} \binom{n-k-1}{l-1} \cdot (n-1)^{l-1} & ({\rm 二項係数をほぐす})\\ &= n^{n-k} - (n-k) \sum_{l=0}^{n-k-1} \binom{n-k-1}{l} \cdot (n-1)^{l} & (l=l+1 {\rm と変換})\\ &= n^{n-k} - (n-k) (n-1+1)^{n-k-1} & ({\rm 二項定理})\\ &= n^{n-k} - (n-k) n^{n-k-1} & \\ &= k \cdot n^{n-k-1} & \end{align*}$

証明 6 (母関数とラグランジュの反転公式) [1]

$n$ 頂点からなるラベル付きの根付き木の総数を $R(n)$ とします。便宜上 $R(0) = 0$ とします。

根なし木を固定したとき根の選び方は $n$ 通りなので、 $R(n) = n T(n)$ となります。 $R(n) = n^{n-1}$ を示すのが目標です。

根の選び方は $n$ 通りあります。

根の子の個数を $m$ に固定します。

子に順番があると考え、それぞれの部分木の大きさが左から順に $k_{1}, k_{2}, \ldots, k_{m} (k_{1} + k_{2} + \ldots + k_{m} = n-1)$ であるとします。

根の子の部分木について、どのラベルを割り当てるかが $\frac{(n-1)!}{k_{1}! k_{2}! \ldots k_{m}!}$ 通りあります。

各部分木について根付き木の作り方はそれぞれ $R(k_{1}), R(k_{2}), \ldots, R(k_{m})$ 通りあります。

子の順番を取り除くために、これらの積を $m!$ で割る必要があります。

以上より

$\begin{align*} R(n) &= n \sum_{m=0} \frac{1}{m!} \sum_{k_{1} + k_{2} + \ldots + k_{m} = n-1} \frac{(n-1)!}{k_{1}! k_{2}! \ldots k_{m}!} R(k_{1}) \cdot R(k_{2}) \cdot \ldots \cdot R(k_{m}) \\ &= \sum_{m=0} \frac{1}{m!} \sum_{k_{1} + k_{2} + \ldots + k_{m} = n-1} \frac{n!}{k_{1}! k_{2}! \ldots k_{m}!} R(k_{1}) \cdot R(k_{2}) \cdot \ldots \cdot R(k_{m}) \\ \end{align*}$

という漸化式が成り立つことが分かります。

次に $R(n)$ の指数型母関数

$\displaystyle f(x) = \sum_{n=0}^{\infty} \frac{ R(n) x^n }{ n! }$

を考えます。

$\begin{align*} x e^{f(x)} &= x \sum_{m=0}^{\infty} \frac{ f(x)^m }{ m! } \\ &= x \sum_{m=0}^{\infty} \frac{1}{m!} (\sum_{n=0}^{\infty} \frac{ R(n) x^n }{ n! })^m \\ &= x \sum_{m=0}^{\infty} \frac{1}{m!} \sum_{k_{1}=0}^{\infty} \sum_{k_{2}=0}^{\infty} \cdots \sum_{k_{m}=0}^{\infty} \frac{1}{k_{1}! k_{2}! \ldots k_{m}!} R(k_{1}) \cdot R(k_{2}) \cdot \ldots \cdot R(k_{m}) x^{k_{1} + k_{2} + \ldots + k_{m}} \\ &= \sum_{m=0}^{\infty} \frac{1}{m!} \sum_{k_{1}=0}^{\infty} \sum_{k_{2}=0}^{\infty} \cdots \sum_{k_{m}=0}^{\infty} \frac{1}{k_{1}! k_{2}! \ldots k_{m}!} R(k_{1}) \cdot R(k_{2}) \cdot \ldots \cdot R(k_{m}) x^{k_{1} + k_{2} + \ldots + k_{m}+1} \\ &= \sum_{m=0}^{\infty} \frac{1}{m!} \sum_{k_{1}=0}^{\infty} \sum_{k_{2}=0}^{\infty} \cdots \sum_{k_{m}=0}^{\infty} \frac{(k_{1} + k_{2} + \ldots + k_{m} + 1)!}{k_{1}! k_{2}! \ldots k_{m}!} R(k_{1}) \cdot R(k_{2}) \cdot \ldots \cdot R(k_{m}) \frac{x^{k_{1} + k_{2} + \ldots + k_{m}+1}}{(k_{1} + k_{2} + \ldots + k_{m} + 1)!} \\ &= f(x) \end{align*}$

最後の等式は先ほどの漸化式から従います。

よって、 $R(n)$ の指数型母関数 $f(x)$ は $f(x) = x e^{f(x)}$ という単純な方程式に従うことがわかりました。

次にラグランジュの反転公式を使います。

ラグランジュの反転公式とは、べき級数

$\displaystyle f(x) = a + \frac{a_{1}}{1!} x + \frac{a_{2}}{2!} x^{2} + \ldots$

が

$\displaystyle f(x) = a + x \phi( f(x) )$

という方程式を満たすとき、

$\displaystyle a_{n} = \left| \frac{{\rm d}^{n-1}}{{\rm dt}^{n-1}} (\phi(t)^n) \right|_{t=a}$

を満たすというものです。

これに先ほどの方程式を当てはめます。

（本当は収束性などを調べないといけないはずですが、参考文献では特に言及されていませんでした。実際 $R(n) = n^{n-1}$ なので収束半径は $\frac{1}{e}$ になるはずなのですが、答えを使わずに証明する良い方法が思いつかなかったのでここでは省略します。僕が勘違いしていたり、良い方法があったりしたら教えてください）