シュトラッセンのアルゴリズムとその導出の仕方

$O(n^{3})$ よりも小さい時間計算量 $O(n^{\log_{2} 7}) \approx O(N^{2.807})$ で行列積を計算するシュトラッセンのアルゴリズムとその導出方法を紹介します。

シュトラッセンのアルゴリズム

$n \times n$ の行列積 $A B = C$ を考えます。

まず $A, B, C$ を

$$ \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix} \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix} = \begin{pmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{pmatrix} $$

というように $\frac{n}{2} \times \frac{n}{2}$ 行列に分解します。

$n$ が奇数のときは余った行、列を適当にどちらかに分けてあげてください。

まず $7$ つの行列積

$$ \begin{align} P_{1} &= ( A_{11} + A_{22} ) ( B_{11} + B_{22} ) \\ P_{2} &= ( A_{21} + A_{22} ) B_{11} \\ P_{3} &= A_{11} ( B_{12} - B_{22} ) \\ P_{4} &= A_{22} ( B_{21} - B_{11} ) \\ P_{5} &= ( A_{11} + A_{12} ) B_{22} \\ P_{6} &= ( A_{21} - A_{11} ) ( B_{11} + B_{12} ) \\ P_{7} &= ( A_{12} - A_{22} ) ( B_{21} + B_{22} ) \end{align} $$

を計算します。

すると、 $C$ の各ブロックは

$$ \begin{align} C_{11} &= P_{1} + P_{4} - P_{5} + P_{7} \\ C_{12} &= P_{3} + P_{5} \\ C_{21} &= P_{2} + P_{4} \\ C_{22} &= P_{1} + P_{3} - P_{2} + P_{6} \end{align} $$

となります。

この証明は両辺を頑張って展開して一致することを確かめればできます。

ここで、各 $P_{i}$ を計算するときに、再帰的にこのアルゴリズムを適用することを考えます。

各ステップの計算は再帰部分以外は行列の加減算なので、 $O(n^{2})$ でできます。

再帰は大きさが半分の問題を $7$ 回呼び出しています。

よって、 Master theorem より、全体の計算量は $O(n^{\log_{2} 7}) \approx O(N^{2.807})$ です。

導出方法

$P_{i}$ と $C_{ij}$ の式が与えられれば証明は頑張って計算するだけですが、 $P_{i}$ と $C_{ij}$ の式がどうやって出てきたのか分かりません。

ここでは簡単な（とはいっても骨の折れる）導出方法を一つ紹介します。

流れは以下のとおりです。

$2 \times 2$ の実行列の掛け算で、要素同士の掛け算を $7$ 回することを目指す
平面上の $120$ 度回転を表す行列 $D$ をとる
非零ベクトル $u$ をとる
$u$ と直交して $u^{\bot} D u = 1$ を満たす横ベクトル $u^{\bot}$ をとる
$X = u u^{\bot}$ とする
$\{ D, X, D^{-1}XD, DXD^{-1} \}$ と $\{ D^{-1}, X, D^{-1}XD, DXD^{-1} \}$ は $2 \times 2$ の行列の基底になっている
$A, B$ をそれぞれ上の基底で表現してかけると $7$ 回ですむ
$D$ は実は固有多項式が同じなら同じ議論が成り立つので、簡単な行列をとってみる
$u$ も簡単なベクトルをとってみる
すると実は 7 はシュトラッセンのアルゴリズムと同じだった

長いですね。

一つずつ見ていきましょう。

回転行列 $D$

$120$ 度 ( $2/3 \pi$ ) の回転行列

$$ D = \begin{pmatrix} -\frac{1}{2} & -\frac{\sqrt{3}}{2} \\ \frac{\sqrt{3}}{2} & -\frac{1}{2} \end{pmatrix} $$

を取ります。

$tr(D) = -1$ , $det(D) = 1$ なので、固有多項式は $\lambda^{2} + \lambda + 1$ です。

ケーリーハミルトンの定理より $D^{2} + D + E = 0 \cdots (1)$ が成り立ちます。

両辺に $D$ をかけると　 $D^{3} + D^{2} + D = 0 \cdots (2)$ が成り立ちます。

(1) と (2) の左辺どうしは等しいので $D^{3} = E \cdots (3)$ となります。これは、 $D$ が $120$ 度の回転行列であることを考えると当たり前のことです。

(3) より $D^{-1} = D^{2} \cdots (4)$ です。

よって、 (1) は $D^{-1} + D + E = 0 \cdots (5)$ と書き換えられます。

(5) より $tr(D^{-1}) = -tr(D) - tr(E) = 1 - 2 = -1 \cdots (6)$ となります。

非零ベクトル $u$

非零ベクトル $u$ をとります。

$u$ と直交する非零の横ベクトル $u'$ をとります。

$D$ の固有多項式の実根は存在しないので、 $u$ は $D$ の固有ベクトルではありません。

よって、 $Du$ は $u$ と別方向を向いているはずなので、 $u'Du \neq 0$ です。

$u^{\bot} = \frac{u'}{u'Du}$ とします。

$u^{\bot}$ は $u$ と直交し $u^{\bot} D u = 1$ となります。

行列 $X$

$X = u u^{\bot}$ をとります。ここで、

$X^{2} = (u u^{\bot}) (u u^{\bot}) = u (u^{\bot} u) u^{\bot} = 0 \cdots(7)$

$XDX = (u u^{\bot}) D (u u^{\bot}) = u (u^{\bot} D u) u^{\bot} = u u^{\bot} = X \cdots(8)$

$XD^{-1}X = (u u^{\bot}) D^{-1} (u u^{\bot}) = u (u^{\bot} D^{-1} u) u^{\bot} = -u u^{\bot} = -X \cdots(9)$

が成り立ちます。

一次独立性

前々節でも言ったように、 $D$ の固有多項式の実根は存在しないので、 $u$ は $D$ の固有ベクトルではありません。

よって、 $u$ と $Du$ は一次独立です。

同様に $u^{\bot}$ と $u^{\bot} D$ は一次独立です。

よって、これらの積 $u \cdot u^{\bot}, u \cdot u^{\bot} D, Du \cdot u^{\bot}, Du \cdot u^{\bot} D$ は $2 \times 2$ 行列の基底になります。

これらに両側から $D$ を掛けます。

$D^{-1} = D^{2} \cdots (4)$ を考えると、 $DXD, DXD^{-1}, D^{-1}XD, D^{-1}XD^{-1}$ となります。

$D$ は正則なので、これらも $2 \times 2$ 行列の基底になります。

これらを足し合わせると $(D + D^{-1}) X (D + D^{-1}) = (-E) X (-E) = X$ となります。ひとつ目の等号は $D^{-1} + D + E = 0 \cdots (5)$ から従います。

よって、基底のうち一つを $X$ で置き換えても基底になります。

これより、 $X, DXD^{-1}, D^{-1}XD$ は一次独立です。

基底表現

$X, DXD^{-1}, D^{-1}XD$ のトレースはそれぞれ、

$tr(X) = tr(u^{\bot}u) = tr(uu^{\bot}) = 0$

$tr(DXD^{-1}) = tr(XD^{-1}D) = tr(X) = 0$

$tr(D^{-1}XD) = tr(XDD^{-1}) = tr(X) = 0$

となります。

よって、 $\{ X, DXD^{-1}, D^{-1}XD \}$ から生成される $2 \times 2$ 行列の部分空間の要素のトレースは $0$ です。

$tr(D) = -1, tr(D^{-1}) = -1$ より、これらはそれぞれ $X, DXD^{-1}, D^{-1}XD$ と一次独立です。

よって、 $\{ D, X, D^{-1}XD, DXD^{-1} \}$ と $\{ D^{-1}, X, D^{-1}XD, DXD^{-1} \}$ はそれぞれ $2 \times 2$ 行列の基底になっています。

$$ A = a_{1} D + a_{2} X + a_{3} D^{-1}XD + a_{4} DXD^{-1} $$

$$ B = b_{1} D^{-1} + b_{2} X + b_{3} D^{-1}XD + b_{4} DXD^{-1} $$

と表します。このとき基底同士の掛け算は

f:id:joisino:20170903160923p:plain

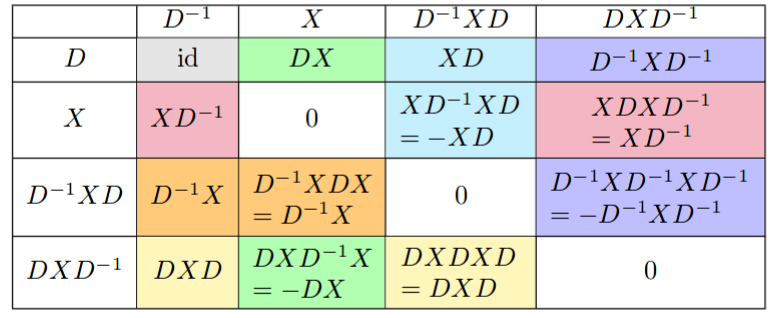
となります。ここでは (7), (8), (9) の結果をたくさん使っています。（表は [2] より引用）

同じ結果が同列、同行に現れているので、これらはまとめられます。

つまり、

$$ \begin{align} AB &=& a_{1} &\times& b_{1} &\times& id \\ &+& a_{2} &\times& ( b_{1} + b_{4}) &\times& XD^{-1} \\ &+& a_{3} &\times& ( b_{1} + b_{2}) &\times& D^{-1}X \\ &+& a_{4} &\times& ( b_{1} + b_{3}) &\times& DXD \\ &+& ( a_{1} - a_{4}) &\times& b_{2} &\times& DX \\ &+& ( a_{1} - a_{2}) &\times& b_{3} &\times& XD \\ &+& ( a_{1} - a_{3}) &\times& b_{4} &\times& D^{-1}XD^{-1} \cdots (10) \end{align} $$

となります。