時間計算量 <O(n), O(1)> の LCA(Lowest Common Ancestor) と RMQ(Range Minimum Query) を C++ で実装しました。
アルゴリズムの解説はDさんのスライド [1] LCA and RMQ ~簡潔もあるよ!~ がとても分かりやすいのでそちらを参照してください。
概要だけ説明します。
LCA の概要
LCA は頂点を dfs 順で訪れた順に並べると深さの列の RMQ に帰着されます。このことは [2] 蟻本 などに載っています。
この列は隣り合う数の差がちょうど になっています。
この列を 個ずつのブロックに分け、それぞれのブロック内の最小値を求めます。
ブロックの数は 個になるので、ブロックの区間の最小値を求めるクエリは sparse table を使うと前処理
、クエリ
で処理できます。
ブロックの中についてですが、各ブロックは 1 つ目の数がわかればあとは +1 されるか -1 されるかの 2 通りです。この遷移の種類は高々 個しかありません。
この全ての種類について、最初の数が だと思って愚直に前計算すると全て合わせて
で計算できます。
あとはクエリが来た時に、完全に含まれるブロックを sparse table で処理して、はみ出た部分を前計算した表を参照して答えればよいです。
RMQ の概要
列を Cartesian Tree という木に変換します。
Cartesian Tree は、列のインデックスをノードの値にもつ二分探索木で、列の値についてヒープ条件を満たしています。ヒープ条件を満たしているとは、列の値について、親の値が子の値以下であるということです。
Treap のような感じです。
すると、RMQ はこの Cartesian Tree 上の LCA クエリに帰着されることがわかると思います。
Cartesian Tree の構成の仕方は [1] には載っていないので少し詳しく説明します。
Cartesian Tree を O(n) で構成する
列を左から右に見ていって、順に Cartesian Tree を構成していきます。
今まで構成した Cartesian Tree の頂点の親を配列で管理し、根から右の子を辿るパスをスタックで管理します。
新しく列の最後に値を追加するとします。
このとき、二分探索木の条件から、新しい頂点はスタックで管理されているパス上の頂点の右の子になるか、根になるかのどちらかです。
どの頂点の子になるかは、スタックの頂点の値よりも新しい頂点の値の方が小さければ、スタックから頂点を取り除くことを繰り返し、最終的にスタックの一番上に残っている頂点が新しい頂点の親になります。スタックが空ならば新しい頂点は根になります。
新しい頂点のせいで親から引き離された頂点は、新しい頂点の左の子にすればよいです。
例えば 4, 2, 5, 1, 3, 8, 7, 9 の後ろに 6 を付け加える場合は以下のようになります。
ノードは (index, val) のように表しています。赤いノードがスタックで管理されているパスです。
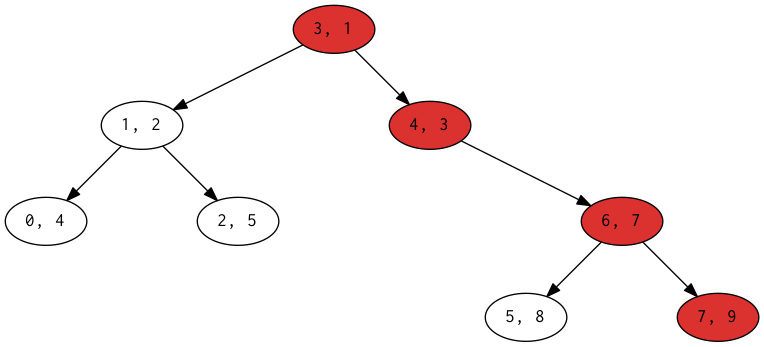
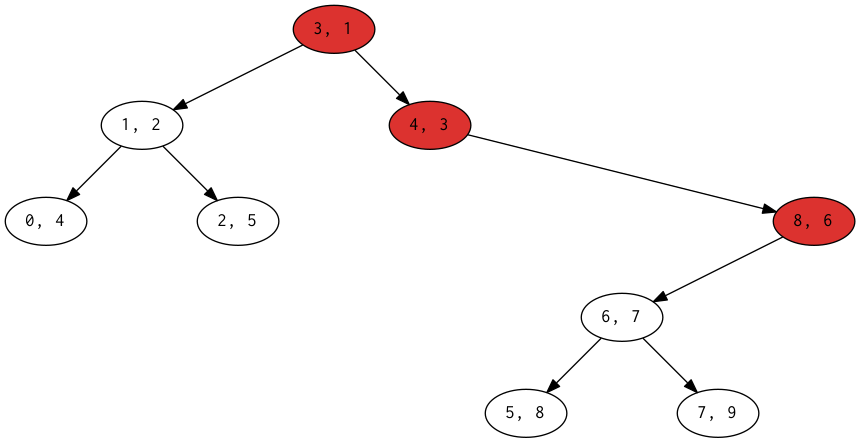
実装
C++ で実装しました。
RMQ
LCA は GRL_5_C に投げたところ、 頂点
クエリで AOJ 上で
0.06s でした。入出力にもある程度時間がかかっていると思います。
RMQ の方は、DSL_3_D (スライド最小値) に投げたところ、 要素
クエリで AOJ 上で
0.34s でした。 RMQ は何段階も帰着させている分線形とはいえ遅いです。
メルセンヌツイスタで生成した乱数に対して RMQ を実行すると、手元の環境だと
要素
クエリで
0.425s要素
クエリで
5.206s
でした。
最後に
何か間違いや質問などがあればお願いします。
最後まで読んでいただきありがとうございました。
参考文献
[2] 秋葉拓哉. 岩田陽一. 北川宜稔. (2012). プログラミングコンテストチャレンジブック [第2版]. pp.294 - 295.